В статье мы рассмотрим понятие "вероятность события случайного". Известно, что в различных сферах деятельности человека и происходят явления, которые невозможно точно спрогнозировать. Так, к примеру, объём продаж продукции зависит как от сильно меняющихся потребностей покупателей, так и от иных нюансов, которые учесть не представляется возможным. Именно поэтому, создавая производство и осуществляя продажи, владельцам приходится предсказывать исход своей деятельности на базе либо личного опыта, либо аналогичного навыка других людей.
Для оценки рассматриваемого события нужно учитывать или специально создавать условия, в которых оно фиксируется. Подобные действия называются опытом или экспериментом. В его процессе возможны эпизоды, которые называют случайными, если в итоге они могут состояться или не состояться, а также достоверные явления, возникающеие в результате практики.
Изучим вероятность события на примерах. Скажем, выпадение в Москве снега 25 ноября считается случайным эпизодом. Каждодневный восход Солнца является достоверным явлением, а выпадение на экваторе снега рассматривается как невозможный курьёз. Одной из главнейших задач в теории вероятностей является проблема определения количественной меры возможности возникновения события.
Вероятность
Вероятностью называют степень (количественную оценку, относительную меру) возможности наступления какого-либо события. Когда же основания для того, чтобы некоторое возможное явление произошло в реальности, перевешивают контрастные аргументы - этот случай называют вероятным. Иначе его именуют сомнительным либо невероятным.
Перевес отрицательной основы над положительной, и наоборот, может быть в разной степени, в силу чего недопустимость (или допустимость) бывает меньшей или большей. По этой причине зачастую вероятность события воспринимается на первоклассном уровне, особенно в тех пассажах, когда точную количественную оценку дать крайне затруднительно или невозможно. Конечно, осуществимы разные градации уровней шанса.
Анализ вероятности
Кстати, вероятность независимых событий имеет особые параметры. А зондирование шанса с математической позиции комплектует специфическую дисциплину – теорию вероятностей. В этом учении и математической статистике понятие допустимости официализируется как числовое описание эпизода (вероятностная мера либо её значение).
Фактически, это мера на множестве случаев (подмножеств множества элементарных явлений), приобретающая величины от 0 до 1:
- значение 1 отвечает достоверному эпизоду;
- невозможный факт имеет нолевой шанс (обратное почти всегда неверно).
Если допустимость пришествия явления равна p, то риск его инертности равен 1-p. Скажем, вероятность ½ означает одинаковую возможность наступления и ненаступления случая.

Формулировка шанса
Испытание, событие, вероятность – эти переменные крепко связаны наукой. Типичное определение шанса базируется на понятии равновероятности исходов.
В качестве возможности выступает отношение количества финалов, содействующих данному событию, к общему количеству равновозможных завершений. Например, допустимость выпадения «решки» или «орла» при неумышленном подкидывании копейки равна 1/2, если рассчитано, что лишь эти два пути являются равновероятными.

Это классическое определение шанса можно обобщить на случай неиссякаемого числа потенциальных значений. Например, если какое-либо явление может произойти с равной допустимостью в любой точке (число точек безгранично) некоторой локальной области плоскости (пространства), то риск того, что оно произойдёт в определённой части этой приемлемой сферы, соответствует отношению площади (объёма) этой части к площади (объёму) области всех возможных точек.
Связующее звено
Вероятность события может определяться эмпирически. Это связано с частотой наступления эпизода исходя из того, что при внушительном числе тестов частота должна преследовать объективную степень возможности этого прецендента.
В нынешнем изложении теории вероятностей шанс выявляется аксиоматически, как частный факт абстрактной теории меры множества. Впрочем, между допустимостью, выражающей степень реальности наступления явления, и абстрактной мерой, связующим звеном является именно частота его отслеживания.

Конечно, вероятность появления события в различных процессах возможна. Стохастическое толкование тех или иных явлений широко распространилось в нынешней науке, в частности в эконометрике, статистической физике термодинамических (видимых) систем, где даже в случае детерминированного классического описания движения частиц, конкретное описание всего их устройства не представляется целесообразным и практически возможным. В квантовой физике сами характеризуемые процессы имеют стохастическое естество.
Случайное событие
Конечно же, вероятность появления события в каждом неконтролируемом процессе велика. Что собой представляет непредвиденный случай? Это подмножество множества исходов нечаянного эксперимента. Если же случайное исследование повторяется много раз, частота наступления факта служит оценкой его допустимости. 
Ненамеренное явление, которое никогда не исполнится в результате непроизвольного эксперимента, называется невозможным. Случайный эпизод, который всегда реализуется в результате нежданного эксперимента, называется достоверным. А как характеризуется вероятность независимых событий? Известно, что два случайных факта называют независимыми, если появление одного из них не изменяет допустимость появления другого.
Случайным явлением называют закономерное событие, которое создано с помощью генерирования непроизвольных функций с подстановкой в переменные беспорядочных величин. Заурядная функция генерирования лотерейного числа исполняется инструментами ЭВМ.
Определение
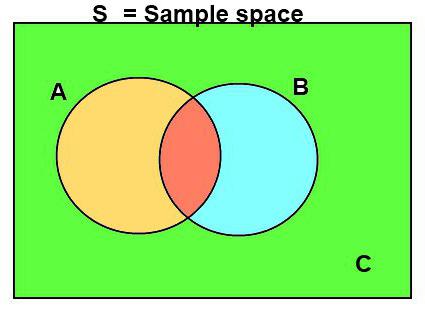
Математически случайным эпизодом является подмножество пространства элементарных исходов непроизвольного испытания. Это элемент сигма-алгебры или алгебры - F, который в свою очередь задаётся самоочевидно и вместе с пространством простейших явлений «Омега» и вероятностью P образует вероятностное пространство.
Предыстория понятия шанса
Вероятность случайного события часто подвергалась исследованиям. Вообще, появление понятия шанса исторически связано с азартными играми, особенно с игрой в кости. До возникновения этого понятия, в основном излагались комбинаторные задачи подсчёта числа потенциальных итогов при метании пары костей, а также вопрос распределения ставки между участниками, когда игра заканчивалась досрочно.
Епископ Виболд из города Камбрэ в 960 году решил первый ребус при бросании трёх костей. Он насчитал 56 видов. Однако это число по сути не воспроизводит сумму равновозможных способов, ведь каждая их 56 версий может осуществляться разным количеством приёмов.
Вероятность случайного события изучал в первой половине 13 века и Ришар де Форниваль. Несмотря на то что у него тоже упоминается число 56, он в размышлениях учитывает, что идентичное число очков на трёх костях можно обрести шестью методами.
Базируясь на его рассуждениях уже можно установить, что количество равнодоступных вариантов – 216. Впоследствии многие решали эту задачу не совсем правильно. Впервые чётко число равнодоступных исходов при подкидывании трёх костей подсчитал Галлилео Галилей: он возвёл шестёрку (количество версий выпадения одной кости) в степень 3 (число костей). Он же составил таблицы числа вариантов извлечения разнообразных сумм очков.
Надеемся, что наша статья в полной мере ознакомила вас с вероятностью события случайного.
